Uitwerken dubbelintegralen
Oorspronkelijke vraag Bereken de integraal $\int_0^{\sqrt{3}}\int_{\frac{y}{\sqrt{3}}}^{\sqrt{4-y^2}}e^{-x^2-y^2}\,\textrm{d}x\d y$
- Schrijf $e^{-x^2-y^2}$ in poolcoördinaten.
Dan is
Antwoord
- Gegeven is de integraal $\int_0^1\int_0^{\sqrt{3}x}\exp(-x^2-y^2)\d y \d x$. Schets het gebied waarover geïntegreerd wordt.
Antwoord
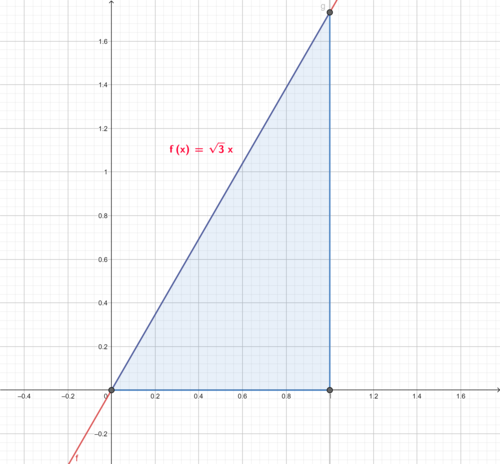
- Gegeven is de integraal $\int_0^1\int_0^{\sqrt{3}x}\exp(-x^2-y^2)\d y \d x$ waarbij wordt overgegaan op poolcoördinaten. Geef de grenzen voor $\theta$ en $r$.
en
Antwoord
en
- Welke integratiemethode zal je gebruiken om de integraal $\int_0^2e^{-r^2}r\d r$ uit te rekenen?
- Substitutie van $r^2 = t$
- Partiële integratie
- Niet op te lossen met de gekende methoden
Antwoord De manier die hier gebruikt moet worden om de integraal te berekenen is de substitutie. Partiële integratie lijkt op het eerste zicht ook een optie, maar als snel zullen problemen opduiken bij het berekenen van $\int e^{-r^2}$, door het ontbreken van een factor $r$.
Opmerking Bij het verder uitwerken van deze integraal kunnen dezelfde vragen gesteld worden als bij het onderdeel integralen.
Bespreking
De meest efficiënte manier om deze gegeven integraal op te lossen is door over te gaan op poolcoördinaten. De opgave kan echter vereenvoudigd worden zodat poolcoördinaten niet langer nodig zijn. Mochten in het integrandum een extra factor $x$ en $y$ staan, kan de dubbelintegraal in een eerste stap gesplits worden als product van twee enkelvoudige integralen en hierna kan rechtstreeks substitutie van $r^2 = t$ worden toegepast.
Ter illustratie Gegeven is de integraal $\int_0^1\int_0^{\sqrt{3}x}e^{-x^2-y^2}xy\,\textrm{d}y\d x$. Het integrandum $f(x,y)$ is te schrijven als $f(x)g(y)$, of dus de veranderlijken kunnen gescheiden worden. Dit betekent dat de integraal als volgt kan herschreven worden:
$\int_0^1\int_0^{\sqrt{3}x}e^{-x^2-y^2}xy\,\textrm{d}y\d x = \int_0^1e^{-x^2}x\,\textrm{d}x\int_0^{\sqrt{3}x}e^{-y^2}y\d y$.
Door de extra factor $x$ en $y$ kan nu enerzijds de substitutie $x^2 = u$ en anderzijds de substitutie $y^2 = t$ worden doorgevoerd. Dit geeft $\left(-\frac{1}{2}\int_0^1e^{-u}\d u\right)\left(-\frac{1}{2}\int_0^{\sqrt{3}x}e^{-t}\d t\right)$. Beide integralen kunnen gemakkelijk berekend worden.
