Voorbeeld

Terug

Beschouw de krommen $K_1$ en $K_2$ in het $xy$-vlak met als vergelijkingen $K_1: f_1(x) = \frac{1}{x^2+1}$ en $K_2: f_2(x) = \frac{x^2}{2}.$ De grafieken van de krommen zijn hieronder weergegeven.

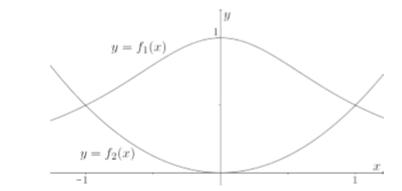
Bereken de oppervlakte van het gebied begrensd door de twee krommen.

Opsplitsing in atomaire vragen

  1. Welke vergelijking moet opgelost worden om de snijpunten van de krommen $K_1$ en $K_2$ te bepalen?

Antwoord $\frac{1}{x^2+1} = \frac{x^2}{2}$.

  1. Gegeven is de vergelijking $\frac{1}{x^2+1} = \frac{x^2}{2}$. De oplossing van deze vergelijking wordt gegeven door $x= \underline{\hspace{1.5em}}$ of $x = \underline{\hspace{1.5em}}$.

  2. Gegeven is dat de krommen $K_1$ en $K_2$ elkaar snijden in de punten (-1,1/2) en (1,1/2). Welke uitdrukking zal berekend moeten worden om de oppervlakte tussen beide krommen te bepalen?

$$ \int_{\dots}^{\dots}\dots \,\textrm{d}x - \int_{\dots}^{\dots}\dots \,\textrm{d}x $$
  1. Bepaal de waarde van de uitdrukking $\frac{1}{2}\left[\frac{x^3}{3} \right]$ tussen de grenzen -1 en 1.

  1. De integraal $\int_{-1}^1 \frac{1}{x^2+1}\,\textrm{d}x$ is gelijk aan \underline{\hspace{3em}}.

  2. Bepaal de waarde van de uitdrukking $Bgtan x$ tussen de grenzen -1 en 1.

  1. Gegeven zijn de krommen $K_1$ en $K_2$ zoals te zien is in de figuur. De oppervlakte onder $K_1$ tussen $x=-1$ en $x=1$ is $\frac{\pi}{2}$ en deze onder $K_2$ tussen $x=-1$ en $x=1$ is $\frac{1}{3}$. Wat is dan de oppervlakte van het gebied begrensd door de twee krommen?

Oppervlakte gebied = $\underline{\hspace{3em}}$

Merk op dat zowel $\frac{\pi}{2} - \frac{1}{3}$ als $\frac{3\pi-2}{6}$ correcte antwoorden zijn.